Understanding Meshless Methods for FEA and CFD

50 years ago engineering simulation revolutionized the product development process. Engineers were able to subject products to physical forces and verify their performance with the new tool in a virtual environment without extensive manual calculations. Physical testing and prototyping, and the tremendous cost associated with each could be reduced or if not reduced improved with the data gained from simulation studies.

As processing power has improved and mathematical advances have occurred engineering simulation has become an integral part of the design process of complicated engineering challenges.

Meshless Methods are based in Mathmatics

But while engineering simulation is understood to be necessary, the mathematics research involved have focused almost exclusively on the enhancement of the management of increasingly complex solutions rather than the productivity gains for the engineer.  Simulation products continue to be tools limited to expert users and highly experienced specialist.  Simulation is increasingly the bottleneck to the design process.

The Theory of External Approximations

Not all mathematics research has excluded the study of improving the efficiency of the engineer. One particular area of research is based on breakthrough extensions to the theory of external approximations. External approximations are a generalization of Finite Element Method (FEM) in terms that:

• absolutely arbitrary geometrical shapes can be used as “finite elements”
• basis functions which approximate field of interest in the “element” can be of arbitrary class and are independent of the “element” shape, alternatively to strictly structured polynomials used in conventional FEA

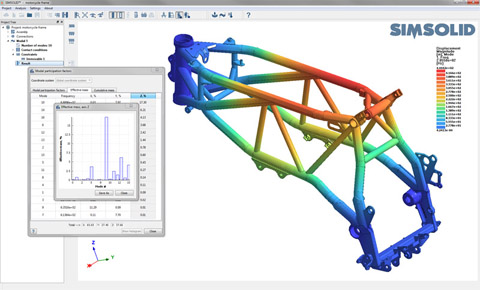
The result is an FEA solution that controls accuracy using multi-pass adaptive analysis. Adaptivity can be defined on a global or part local basis and adaptivity is always active. It provides superior performance metrics for computational time and memory footprint that allow very large and/or complex assemblies to be solved quickly on desktop class PC’s.

FEA Software based on the theory of external approximations includes SIMSOLID. For more details on SIMSOLID, click here.

Moving Particle Semi-implicit Method (MPS Method)

A second area of research is the Moving Particle Semi-implicit Method (MPS Method). This method was developed by Professor Seiichi Koshizuka at the Department of Systems Innovation, and Director of the Koshizuka Lab, at the University of Tokyo, Japan. He has since co-authored 5 books on this topic, and many journal articles on topics across particle simulation, and physics based computer graphics.

The MPS Method is a Lagrangian formulation for approximating the Navier-Stokes equations for non-compressible flow. Particle interaction models are prepared for gradient, divergence and Laplacian and other differential operators . Governing equations are transformed to interactions among moving particles. Therefore the simulation is meshless.

By analyzing the motion of fluids and separating them into sets of freely moving discrete elements (particles), you simulate large deformation, coalescence and segmentation of fluid, and rapid change of flow ? without requiring the complicated pre-process mesh creation. Ths meshless method provides very good performance in the simulation of moving boundary problems - typically a time intensive task for mesh based methods. When dealing with complex structures such as gears and impellers, structures are first translated into polygon models, making it simple to apply detailed movement settings.

CFD software based on the MPS methods includes ParticleWorks. For more details on ParticleWorks, click here.

See more reasearch with the book on Amazon "Moving Particle Semi-implicit Method: A Meshfree Particle Method for Fluid Dynamics" 1st Edition, by Seiichi Koshizuka (Author), Kazuya Shibata (Author), Masahiro Kondo (Author), Takuya Matsunaga (Author).

The RBS Method

The RBF method employs a basis function that relates the influence of surrounding nodes to the node of interest, i.e., a distance, d, with the nodes closest to the node of interest having the greatest influence. The two techniques commonly used in RBF-based methods are based on global versus local collocation. The global approach collocates over the total number of nodes within the computational domain, i.e., the global matrix is defined by the total number of nodes, N, creating an N x N matrix that must be solved. The local approach employs only local collocation, creating a series of overlapping matrices defined by m x m nodes surrounding the node of interest. This creates a small series of linear equations that must be solved for each node. Providing the problem domain and number of nodes are not huge, the global RBF approach works well for simple and small problems.

See more research under Darrell W. Pepper and Maria Ramos Gonzalez; A Localized Meshless Technique for Generating 3-D Wind Fields; MDPI 1 Feb 2018

Need experts in FEA and CFD to assist with your current projects?